同步带水平运动¶

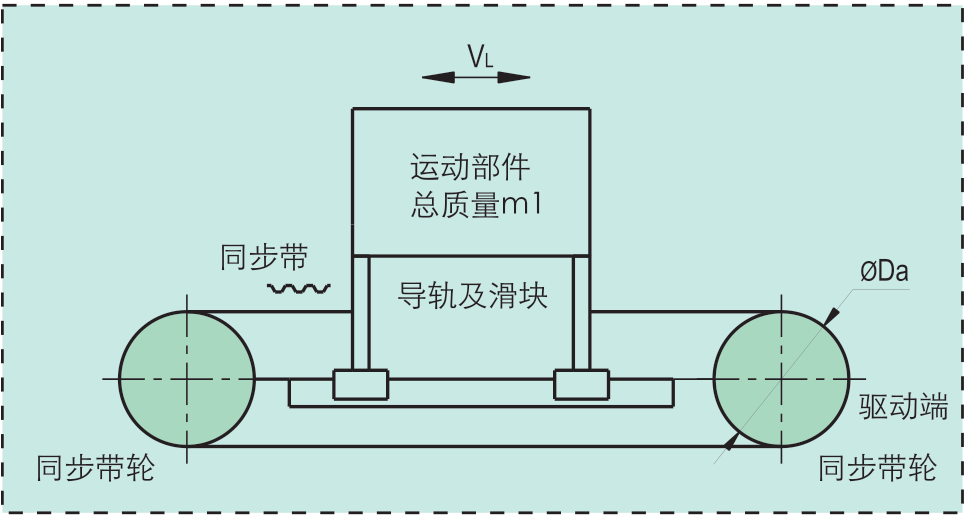
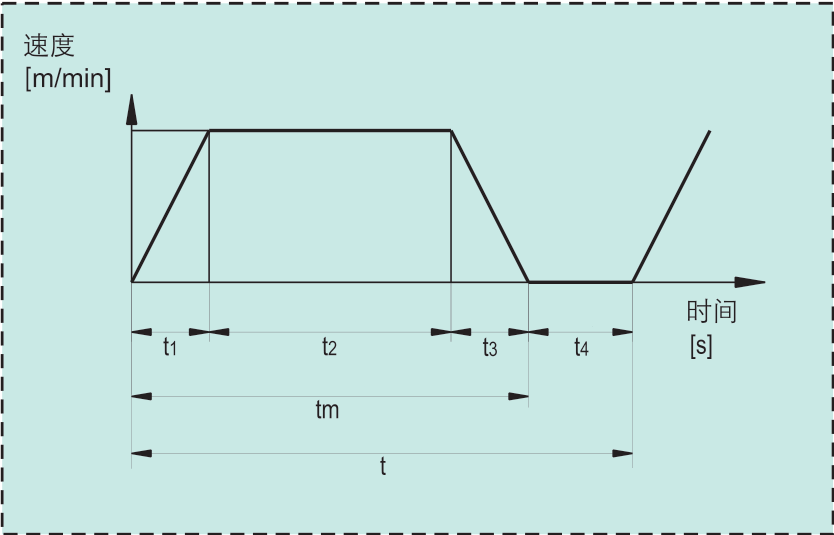
机构模型示意图	时间位移曲线

条件¶

直线运动部的总质量m₁=12kg。
直线运动部的最高速度V_L=72m/min。
电气停止精度δ=±0.05mm。
滑块摩擦系数μ₁=0.1。
机械传动链总效率η₁=0.95。
滚珠丝杆的长度L₁=1.2m。
同步带轮直径D_a=0.08m。
同步带轮宽度w=25mm。
每个同步带轮的质量m₂=0.32kg。
运行周期t=1.5s。
加减速时间t₁=t₃=0.1s。

计算¶

运动曲线¶

由： $$ L_1 =\frac{1}{2}\times \frac{V_L}{60}\times t_1+\frac{V_L}{60}\times t_2+\frac{1}{2}\times \frac{V_L}{60}\times t_3 $$ 推出： $$ t_2=\frac{60\times L_1}{V_L}-t_1=\frac{60\times 1.2}{72}-0.1=0.9s $$ 每分钟运行次数： $$ N_{每分钟运行次数}=\frac{60}{1.5}=40 $$ 加速每分钟运行时间： $$ t_5=t_1\times N =0.1\times 40=4s $$ 每分钟伺服电机加速累计运行时间一般要求在10s以内，条件满足。

计算最高负载转速¶

$$ n_1=\frac{V_L}{\pi \times D_a}=\frac{72}{3.14\times 0.08}≈286.6r/mim $$

计算连续最大负载转矩¶

导轨的摩擦力 $$ F_1=\mu_1 m_1g+F_2=0.1\times 12\times 9.8+30=41.76N\ $$ 滑块的摩擦阻力F₂ ，取F₂=30N

连续最大负载转矩： $$ M_1=\frac{F_1D_a}{2\eta_1}=\frac{41.76\times 0.08}{2\times 0.95}=1.76N.m $$

额定转矩应满足 $$ M_2=S_1\times M_1=1.5\times 1.76=2.64N.m $$ S₁为安全系数，一般S₁≥1.5，取S₁=1.5

计算负载惯量¶

直线运动部的转动惯量： $$ J_1=\frac{m_1\times {D_a}^2}{4}=\frac{12\times 0.08^2}{4}=0.019kg.m^2 $$ 同步带轮的转动惯量： $$ J_2=\frac{m_2\times {D_a}^2}{8}=\frac{0.32\times 0.08^2}{8}=2.56\times 10^{-4}kg.m^2 $$ 负载惯量 $$ J_3=J_1+2J_2=0.019+2\times 2.56\times10^{-4}=195.12\times 10^{-4}kg.m^2 $$

计算加速瞬时转矩¶

最大加速瞬时转矩： $$ M_3=\frac{2\pi \times n_1\times J_3}{60\times t_1}+M_1 =\frac{2\times 3.14\times 286.6\times 195.12\times 10^{-4}}{60\times 0.1}+1.76 =7.6N.m $$ 瞬间转矩应满足： $$ M_4=S_2\times M_3=2\times 7.6=15.2N.m $$ S₂为安全系数，一般S₂≥2，取S₂=2

选型¶

查看伺服电机手册参数：

额定转速n_m＞n₁，

额定转矩M_m1＞M₂，

瞬间转矩M_m2＞M₄，

减速比i。

伺服电机转子惯量J_m，伺服电机转子惯量用与计算惯量比，一般推荐惯量比小于20。

惯量比¶

$$ J_R=\frac{J_4}{J_m\times i^2} $$

一般推荐惯量比小于20。

标准法兰伺服减速电机径向负载验算¶

同步带预紧力，由工况取F3=70N

加速瞬间转矩产生的切向力 $$ F_4=\frac{2\times M_4}{D_a}=\frac{2\times 15.2}{0.08}=380N $$ 减速机输出端承受的径向力 $$ F_5=F_3+F_4=70+380=450N $$ 查标准法兰轴向容许负载表，径向容许负载

。。。。。。。。。。。。。。

123